機械もすなる論理学を機械にやらせてみた
TL;DR: Prologの双方向代入最高!
はじめに
8年ほど前に『論理学を作る』という本を読みまして、そこにタブローの方法と呼ばれる論理式の集合が充足可能か調べるアルゴリズムが載っていました。「暇があったらいつか実装してみるか」と思っていたら8年も経ってしまいましたが、暇があったので実装してみました。Prologで。
タブロー(tableau)とは要は木で、木を書くと論理式の集合が充足可能かどうか分かるというものです。こういう時にはWikipediaさんに説明を任せたいのですが、日本語版にはまるで情報がありません。英語版はきちんと書いてあるっぽいので気になる方はそちらを参照してください。
少しだけ説明をすると、与えられた論理式の集合をルートとして、その中の複合式を充足させるのに必要な(より小さな)式を子として木を作っていき、ルートからリーフに至る経路にAと¬A (Aはリテラル) の両方が現れなければ充足可能。すべての経路にAと¬Aの両方が現れたら矛盾とわかるという仕組みです。
例えば論理式の集合 {A∨B, ¬A} に対してタブローを描くと次のようになります(記号は適切に読み替えてください)。
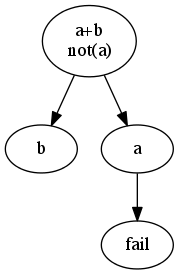
A∨Bを充足させるためにはAかBが真になる必要があります。しかし、¬Aがあるので、Aは真には出来ません(右の経路)。しかしBが真になれるのでこの集合は充足可能です(左の経路)。
はい、ようやくPrologの話です
さて、この図ですが、Prologで書きました。
?- tableau([a+b, not(a)], R).
digraph tableau {
node101 [ label = "b\n" ];
node100 [ label = "fail\n" ];
node99 [ label = "a\n" ];
start [ label = "a+b\nnot(a)\n" ];
start -> node101
node99 -> node100
start -> node99
}
R = ok.
述語tableauの第一引数に論理式の集合を入れてやると、DOT言語を出力するので、こいつを dot コマンドに入れてやると図が出てくるという仕組みです。変数Rが ok というのは充足可能という意味です。入力に ¬B を加えてやると矛盾となり、Rには fail が入ります。
?- tableau([a+b, not(a), not(b)], R). (中略) R = fail.
もっと複雑な入力を入れてみましょう。集合 {A→B, B→C, C→D, ¬(A→D)} が充足可能か調べます。
?- tableau([a->b, b->c, c->d, not(a->d)], R).R = fail.
はい。見事に矛盾していると見抜けました。やったね。
Prologといえば双方向代入
これだけなら「どんなプログラミング言語で書いても一緒だろ」という物言いが付きそうなので、Prologならではのことをやってみようと思います。先ほどの集合 {A→B, B→C, C→D, ¬(A→D)} は少しいじれば充足可能に出来そうです。そこで A→B の A の部分を何か別の論理式に変えることを考えてみましょう。つまり {α→B, B→C, C→D, ¬(A→D)} が充足可能となるような α を見つけましょう。
タブローを作るプログラムしか書いていない場合、多くのプログラミング言語ではこのようなことをするために新たにプログラムを書き足す必要がありそうですが、Prologではプログラムを一切書き換えること無くこのようなことが出来ます。
;;; グラフの出力は省略 ?- tableau([X->b, b->c, c->d, not(a->d)], ok). X = not(a); X = not(not(d)); X = not(not(c)); X = not(not(b)); X = not(not(_G1749)); X = not(a*a); X = not(a*not(d)); X = not(a*not(c)); X = not(a*not(b)); ...
¬A のような単純なものから始まり ¬(A∧¬B) などという少々複雑なものも出てきて面白いです。このまま続けていけば非常に長い式も得られるのですが、 ¬(A∧(A∧(A∧(A∧(A∧(A∧(A∧¬D))))))) のような面白みのないものになってしまいました。
今回は命題論理だけを扱いましたが、『論理学を作る』ではこのあとタブローを述語論理に対応させたりどんどん拡張していくので、こちらも暇があったらやってみようと思います。