関西Coders 第一回ミーティング
4月9日に大阪府池田市某所にて、怪しげな集会に行ってきました。
植木のまち池田
池田城
インスタントラーメン発明記念館
池田ァ！！！！！
＿_, . : ´ ￣￣ ｀ ､
､＿＿, . :´: : : : : : : : : : : : : : : : : . ヽ
＼｀ ＜ . : : : : : : : : : : : : : : : : : : : : : .＼
＼ ｀ヽ､: : : : : : : : : : : : : : : : : : : : : .＼
八＿≦=＼: : : : : ／ . : ＿＿: : : : : : : . ヽ
/ .: : : : : : : : : : : ／ . : ／ /／l : : : : : : . l＼
/ .: : : : : : : : : : ／ ＼／ l/ |ﾉ ヽ: : : : :|: . ヽ
／ .: /: : : : : : : : /＼_／｀＼ | : : : :|: : : . ＼_
_／ .:／/ : : : :/⌒Ｖ. :／｀ヽ ノ￣￣｀ヽ、―ニ 二三
￣￣ / : :／ｌﾊ /: /｀ヽ ／ ´｀ヽ _ 三,:三ー二二
|: :/ ｌ : :/ ／ ノヽ–/￣ , ｀￣￣￣￣
∨ | :/ ∧⊂⊃ﾐ } …| /!ﾍ;;;;丿
＿＿_ ／Ⅳ//∧ _}｀ー‐し’ゝL _
//￣＼＼ |ノ￣＼ヽ ﾍｒ–‐‐’´} ;ー——–
〃￣＼ ＼＼ ＼＼ ヾ:::-‐’ーｒ‐'”＝＝-──
〃 ＼ ＼＼ ヽ ｀ /￣厂｀丶､＿_ ﾚ′
〃 ＼ ＼＼ l＿＿/ // ∧
// ＼ ＞ｰ 、 | / // ／ l
､＿＿, . :´: : : : : : : : : : : : : : : : : . ヽ
＼｀ ＜ . : : : : : : : : : : : : : : : : : : : : : .＼
＼ ｀ヽ､: : : : : : : : : : : : : : : : : : : : : .＼
八＿≦=＼: : : : : ／ . : ＿＿: : : : : : : . ヽ
/ .: : : : : : : : : : : ／ . : ／ /／l : : : : : : . l＼
/ .: : : : : : : : : : ／ ＼／ l/ |ﾉ ヽ: : : : :|: . ヽ
／ .: /: : : : : : : : /＼_／｀＼ | : : : :|: : : . ＼_
_／ .:／/ : : : :/⌒Ｖ. :／｀ヽ ノ￣￣｀ヽ、―ニ 二三
￣￣ / : :／ｌﾊ /: /｀ヽ ／ ´｀ヽ _ 三,:三ー二二
|: :/ ｌ : :/ ／ ノヽ–/￣ , ｀￣￣￣￣
∨ | :/ ∧⊂⊃ﾐ } …| /!ﾍ;;;;丿
＿＿_ ／Ⅳ//∧ _}｀ー‐し’ゝL _
//￣＼＼ |ノ￣＼ヽ ﾍｒ–‐‐’´} ;ー——–
〃￣＼ ＼＼ ＼＼ ヾ:::-‐’ーｒ‐'”＝＝-──
〃 ＼ ＼＼ ヽ ｀ /￣厂｀丶､＿_ ﾚ′
〃 ＼ ＼＼ l＿＿/ // ∧
// ＼ ＞ｰ 、 | / // ／ l
全体のことはいけがみさんが書いてくれたので、
Prologで書いたML(のサブセット)のインタプリタ(?)の話でも書いておきます。
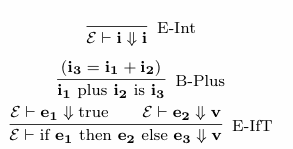
こんな感じの推論規則を元に、
rule(['|-', Env, I, evalto, I], [], 'E-Int') :- env(Env), i(I).
rule([I1, plus, I2, is, I3], [], 'B-Plus') :-
i(I1), i(I2), I3 is I1 + I2.
rule(['|-', Env, [if, E1, then, E2, else, E3], evalto, V],
[['|-', Env, E1, evalto, true],
['|-', Env, E2, evalto, V]], 'E-IfT') :-
e(E1), e(E2), e(E3), env(Env).
こんな感じの述語を定義して、
infer(X, [X, by, Name]) :- rule(X, [], Name). infer(X, [X, by, Name|Z]) :- rule(X, Y, Name), infer_list(Y, Z). infer_list([], []). infer_list([X|Xs], [Y|Ys]) :- infer(X, Y), infer_list(Xs, Ys).
推論規則を次々つかってやる述語を定義すると、
% 心の目で "if true then 1 + 2 else 0 => X" とお読みください
?- infer(['|-', [], [if, true, then, [1, +, 2], else, 0], evalto, X], Z), output(Z).
|- if true then 1 + 2 else 0 evalto 3 by E-IfT {
|- true evalto true by E-Bool {};
|- 1 + 2 evalto 3 by E-Plus {
|- 1 evalto 1 by E-Int {};
|- 2 evalto 2 by E-Int {};
1 plus 2 is 3 by B-Plus {}
}
}
X = 3,
Z = [...]
式の値を求めた上で証明木を書いてくれるというものです。
(証明木は
A B ----- RULE C
を
C by RULE {
A;
B
}
と記述しています)
一応、型推論やら継続の取り扱いなどもできます。
大学院の講義で「導出を書け」という課題があったため作ったもので、手抜きです。
MLのパーサは書いてないので、人間がパース済みの入力を与えるという、
素晴らしき作りになっています。